Turbulence model development
In order to determine the structure temperatures in a spallation target with sufficient accuracy, adequate turbulence models are required to predict the temperature field in the cooling fluid. Standard models, which are used in commercial codes, are not suitable for the simulation of convective heat transfer in heavy liquid metals. This is especially true when buoyancy effects are important. So, it is the general topic of our work to gather experience with the statistical turbulence models which are applied in the commercial codes for the target analysis, and to extend the turbulence models or to develop new ones.
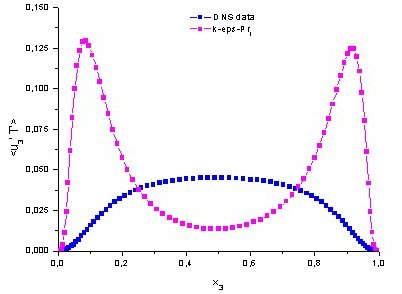 |
| DNS analysis of the turbulent heat flux in the vertical direction in Rayleigh-Bénard convection in Mercury or PbBi at Ra = 100 000. The standard k-eps model with a constant turbulent Prantl number of 0.9 fails qualitatively to predict the correct vertical heat flux distribution. (Otic & Groetzbach 2003) |
The challenge in developing more accurate models is that the measurement capabilities are very limited to provide the required detailed local data, especially cross correlations between velocities, pressure, and temperature fluctuations in liquid metal flows. The following methods are used to gain the data or to provide new numerical simulation possibilities:
DNS: Direct numerical simulation (DNS) of turbulence is the common tool to provide the required understanding of the flow mechanisms and the required data at least for small turbulence Reynolds numbers to develop better turbulence models. The DNS method is based on the complete three-dimensional and time-dependent conservation equations for mass, momentum and energy. Except for the very fine grids, which are required in sufficiently large computational domains, the method does not depend on any other parameters. So the results can be used to investigate any type of turbulence modelling.
- Here we perform DNS with our TURBIT code to extend our DNS data base.
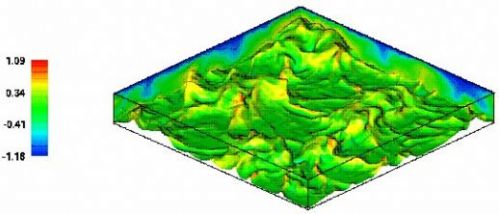
| DNS results for the instantaneous temperature field (isosurface for T=75% of delta-Tmax) and for the vertical velocity (colour code) in Rayleigh-Bénard Convection of Mercury or PbBi at Ra = 100 000. Due to the large thermal conductivity compared to the small viscosity, the temperature field obeys mainly large scale structures, whereas the velocity field contains also much smaller scales of fluid rising in plume-like structures. This is a qualitative indication why the Reynolds analogy does not apply in liquid metals. (Otic & Groetzbach 2003) |
LES: Large eddy simulation (LES) of turbulence means, that only the large and slow scales of turbulence are resolved by the grid and in time. The small scales have to be modelled by sub-grid scale models. Such methods have less sensitivity against model uncertainties than the following RANS models. Important uncertainties occur here in the modelling of flows with areas having thermal stratification in combination with fluids like liquid metals. LES is the preferred method in engineering to investigate prototypic flows and flows which are anyway three-dimensional and locally time-dependent. They are more and more used to investigate thermal striping phenomena or are going to be used for flow induced fluid-structure interaction investigations.
- Here, we analyse our DNS data to develop a new two-equation subgrid scale model for thermal convection in liquid metals for future use in modern CFD codes. The model will be tested within the TURBIT code. The activity was performed within a national cooperation in the ‘Interdisciplinary Turbulence Initiative’ which was fully funded by the DFG.
RANS: Reynolds averaged Navier-Stokes equation based models (RANS) are the working horses in our actual CFD codes. They are basing on the time-averaged equations, so that all turbulence is filtered out and has to be introduced completely by model assumptions. The current commercial codes do not provide special turbulent heat flux models which are suited for liquid metal flows, whereas some of the codes which were developed in the nuclear community, like FLUTAN, have already models with some important improvements which were mainly developed from DNS data.
- Here, we use theoretical means and analyses of our DNS data to develop the required model improvements and new models for the turbulent heat flux in the convection of various fluids, including liquid metals. Later, the models shall be tested and practically investigated either in FLUTAN or in a suitable commercial code.
Thus, our modelling activities concentrate on the following three topics:
- Investigations of basic transport mechanisms in turbulent flows by means of DNS, especially in flows of different fluids including buoyancy phenomena.
- Development of new sub-grid scale models for LES of buoyant flows in various fluids by means of theoretical means and DNS data.
- Development of improved statistical turbulent heat flux models for liquid metal flows by theoretical means and DNS data and implementation in CFD codes.
References:
- Woerner, M., Groetzbach, G., Pressure transport in direct numerical simulations of turbulent natural convection in horizontal fluid layers. Int. J. Heat & Fluid Flow 19 (1998) pp. 150 – 158
- Carteciano, L. N., Woerner, M., Groetzbach, G., Erweiterte Turbulenzmodelle fuer technische Anwendungen von FLUTAN auf Naturkonvektion. Kerntechnische Gesellschaft e.V., INFORUM Bonn (1999) S. 129 – 133.
- Carteciano, L., Groetzbach, G., Validation of turbulence models for a free hot sodium jet with different buoyancy flow regimes using the computer code FLUTAN. Forschungszentrum Karlsruhe, FZKA 6600 (2003)
- Otic, I., Groetzbach, G., Direct numerical simulation and statistical analysis of turbulent convection in lead-bismuth. International Conference on Supercomputing in Nuclear Applications (SNA 2003) Paris, Proc. on CD-ROM, paper Nr. S10/2, CEA, 91191 Gif sur Yvette, Cedex, F.
- Otic, I., Groetzbach, G., Direct numerical simulation and RANS modeling of turbulent natural convection for low Prandtl-number fluids. Computational Technology for Fluid / Thermal / Chemical / Stressed Systems with Industrial Applications, Eds. V. Kudriavtsev, C. R. Kleijn, S. Kawano, ASME, PVP-Vol. 491-2 (2004) Vol. 2, pp. 159-165, ISBN No. 0-7918-4686-5
- Groetzbach, G., Turbulence modeling issues in ADS thermal and hydraulic analyses. IAEA Technical Meeting on Theoretical and Experimental Studies of Heavy Liquid Metal Thermal Hydraulics, Karlsruhe, Germany, Oct. 28-31 (2003). IAEA-TECDOC-1520,IAEA Wien, Oct. 2006, pp. 9-32
- Otic, I., Grötzbach, G., Turbulent heat flux and temperature variance dissipation rate in natural convection in lead-bismuth. Nuclear Science & Engineering 155, pp.489-496 (2007)
- Chandra, L., Grötzbach, G., Analysis and modeling of the turbulent diffusion of turbulent kinetic energy in natural convection. Accepted at Flow, Turbulence and Combustion (2007)
- Grötzbach, G., Anisotropy and buoyancy in nuclear turbulent heat transfer – Critical assessment and needs for modelling. Forschungszentrum Karlsruhe, FZKA 7363, 2007
- Grötzbach,G., Revisiting the Resolution Requirements for Turbulence Simulations in Nuclear Heat Transfer. Nuclear Engineering & Design, Vol. 241, 2011, pp. 4379-4390 DOI: 10.1016/j.nucengdes.2010.12.027
- Grötzbach, G., Challenges in low-Prandtl number heat transfer simulation and modeling. Nuclear Engineering & Design, Vol. 264, 2013, pp. 41-55, Doi: 10.1016/j.nucengdes.2012.09.039
For further references on the TURBIT code, its applications, and new RANS model developments consider the databank of FZK publications and search for the publications of the authors listed above.
Staff members involved:
J. Dumond, J. Fetzer
Contact person:
G. Grötzbach; groetzbach at partner.kit.edu